1) $|A(x)|=k$, con $k< 0$ l’equazione è impossibile.

Esempio:

$|3x^3-2x|=-3$

2) $|A(x)|=k$, con $k> 0$ l’equazione equivale a $A(x)=k$ $\vee$ $A(x)=-k$.

Esempio:

$|x-7|=3$

$x-7=3$ $\vee$ $x-7=-3$

$x=10$ $\vee$ $x=4$.

L’insieme delle soluzioni dell’equazione è $\displaystyle S=\left\lbrace 4,10 \right\rbrace $.

3) $|A(x)|=0$, equivale a $A(x)=0$

Esempio:

$|x-7|=0$

$x-7=0$

$x=7$

L’insieme delle soluzioni dell’equazione è $\displaystyle S=\left\lbrace 7 \right\rbrace $.

4) $|A(x)|=|B(x)|$, equivale a $A(x)= B(x)$ $\vee$ $A(x)=-B(x)$

Esempio

$|2x-2|=|3x-2|$

$2x-2=3x-2$ $\vee$ $2x-2=-3x+2$

$x=0$ $\vee$ $\displaystyle x=\frac{4}{5}$

L’insieme delle soluzioni dell’equazione è $\displaystyle S=\left\lbrace 0,\frac{4}{5}\right\rbrace $.

5) $|A(x)|=B(x)$, equivale a:

$\begin{cases}
A(x)\geq 0 &\\
A(x)=B(x) &
\end{cases}$ $\vee$ $\begin{cases}
A(x)< 0 &\\
-A(x)=B(x) &
\end{cases}$

Esempio

$|x+1|=2x-2$

$\begin{cases}
x+1\geq 0 &\\
x+1=2x-2 &
\end{cases}$ $\vee$ $\begin{cases}
x+1<0 &\\
-(x+1)=2x-2 &
\end{cases}$

$\begin{cases}
x\geq -1 &\\
x=3 &
\end{cases}$ $\vee$ $\begin{cases}
x<-1 &\\
x=\displaystyle \frac{1}{3} &
\end{cases}$

La soluzione $x=3$ è accettabile poiché soddisfa la condizione $x\geq -1$.

La soluzione $\displaystyle x=\frac{1}{3}$ non è accettabile poiché non soddisfa la condizione $x<-1$.

L’insieme delle soluzioni dell’equazione originaria è $S=\{3\}$.

6) Equazioni con più valori assoluti

Esempio

$|x+1|=|x-2|-3x+1$

1) studiamo il segno degli argomenti dei valori assoluti:

$x+1>0$ $\Rightarrow$ $x>-1$

$x-2>0$ $\Rightarrow$ $x>2$

2) costruiamo la tabella dei segni:

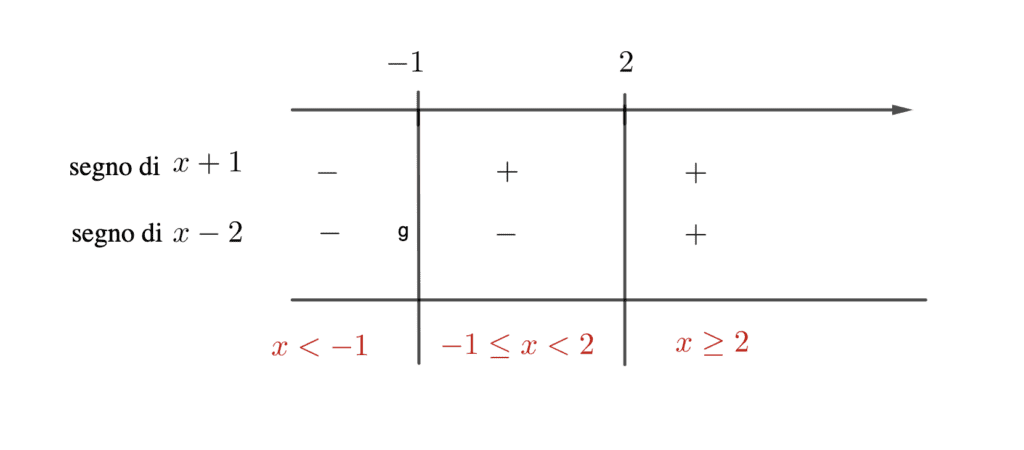
3) scriviamo l’equazione originaria in ogni intervallo, tenendo conto dello studio del segno degli argomenti al punto 2 e della definizione di valore assoluto:

$\begin{cases}
x<-1 &\\
-(x+1)=-(x-2)-3x+1&
\end{cases}$ $\Rightarrow$ $\begin{cases}
x<-1 &\\
\displaystyle x=\frac{4}{3}&
\end{cases}$

$\begin{cases}
-1\leq x<2 &\\
(x+1)=-(x-2)-3x+1&
\end{cases}$$\Rightarrow$ $\begin{cases}
-1\leq x<2 &\\
\displaystyle x=\frac{2}{5}&
\end{cases}$

$\begin{cases}
x\geq 2 &\\
(x+1)=(x-2)-3x+1&
\end{cases}$ $\Rightarrow$ $\begin{cases}
x\geq 2 &\\
\displaystyle x=-\frac{2}{3}&
\end{cases}$

L’insieme delle soluzioni dell’equazione originaria è $\displaystyle S=\left\lbrace \frac{2}{5}\right\rbrace $.