Risolvere la seguente disequazione frazionaria:

$\displaystyle \frac{1}{x^2-x}-\frac{1}{x}\ge\frac{2}{x-1}$

SOLUZIONE

$\displaystyle \frac{1}{x(x-1)}-\frac{1}{x}\ge\frac{2}{x-1}$

$\displaystyle \frac{1}{x(x-1)}-\frac{1}{x}-\frac{2}{x-1}\ge0$

$\displaystyle \frac{1-1(x-1)-2x}{x(x-1)}\ge0$

$\displaystyle \frac{1-x+1-2x}{x(x-1)}\ge0$

$\displaystyle \frac{2-3x}{x(x-1)}\ge0$

Studio del segno:

$N\ge0$:   $2-3x\ge0$;   $\displaystyle x\le\frac{2}{3}$

$D_1>0$:   $x>0$

$D_2>0$:   $x-1>0$;   $x>1$

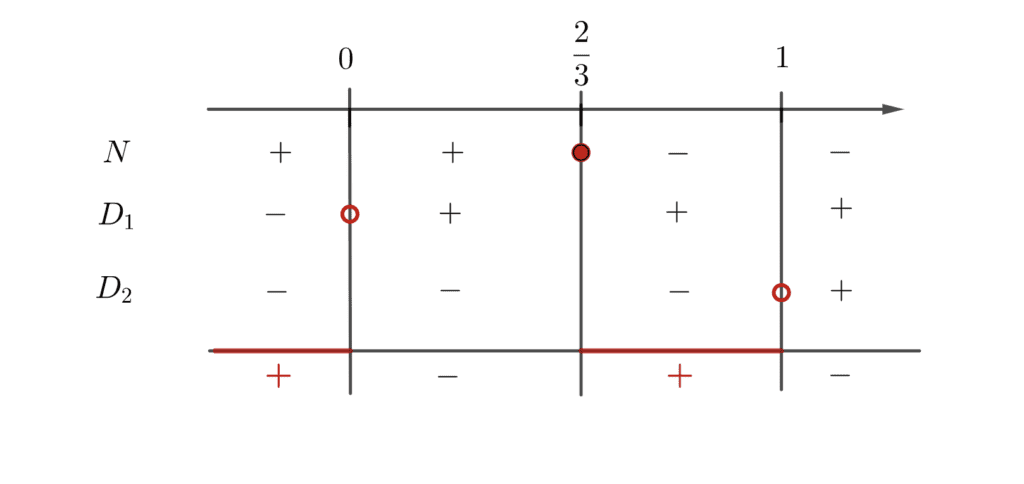
$\displaystyle S=\{x\in \mathbb{R}\:| x<0 \vee \frac{2}{3}\leq x<1\}$