Determinare i punti dell’iperbole $\displaystyle \frac{x^2}{4}-\frac{y^2}{12}=1$ che formano con i fuochi un triangolo di area 12.

SOLUZIONE

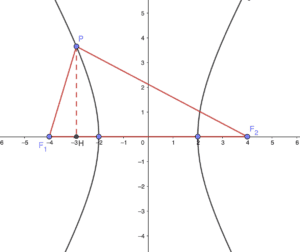
Prendiamo punto generico dell’iperbole con ordinata positiva $P(x, \sqrt{3x^2-12})$.

Consideriamo $H$ la proiezione di $P$ sull’asse $x$ e $PH$ l’altezza del triangolo $PF_1F_2$.

Dalla relazione $c^2=a^2+b^2$, ricaviamo $c=\pm\sqrt{a^2+b^2}=\pm\sqrt{16}=\pm 4$.

La lunghezza della base del triangolo $\overline{F_1F_2}=8$ e l’altezza $\overline{PH}=\sqrt{3x^2-12}$.

Imponiamo l’uguaglianza $\displaystyle 12=\frac{\sqrt{3x^2-12}\cdot 8}{2}$, da cui ricaviamo:

$\displaystyle 3x^2-21=0$, che ha per soluzioni $x=\pm \sqrt{7}$.

I punti sono: $(\sqrt{7}, 3)$, $(-\sqrt{7}, 3)$, $(\sqrt{7}, -3)$, $(-\sqrt{7}, -3)$.